Dots and Boxes

Η Τάμτα και η Άννα είναι αδερφές που παιζουν το γνωστό παιχνίδι με τις Τελείες και τα Κουτιά.

Το παιχνίδι ξεκινάει με ένα άδειο πλέγμα ~(N + 1) \times (M + 1)~ με τελείες (άρα ισοδύναμα ~N \times M~ κουτιά). Οι παίκτες παίζουν εναλλάξ συνδέοντας γειτονικές τελείες κατακόρυφα ή οριζόντια με μία γραμμή (πρέπει να μην υπάρχει ήδη γραμμή μεταξύ τους). Όταν κάποιος δημιουργεί την τέταρτη πλευρά ενός ~1 \times 1~ τετραγώνου, το κερδίζει, αυξάνει το σκορ του κατά 1 και ξαναπαίζει. Το παιχνίδι τελειώνει όταν δεν μπορεί να τοποθετηθεί άλλη ακμή.

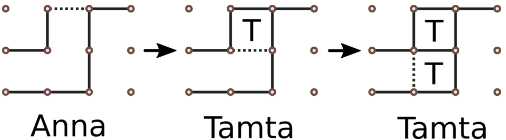
Η Τάμτα και η Άννα παίζουν λίγη ώρα τώρα και έχετε παρατηρήσει ότι στην τρέχουσα κατάσταση κάθε τετράγωνο έχει ακριβώς 0 ή 2 μη-συμπληρωμένες πλευρές και πρόκειται να παίξει η Άννα. (βλ. παράδειγμα παρακάτω. Προσοχή: η παραπάνω εικόνα δεν είναι ορθή κατάσταση)

Το σκορ του παιχνιδιού υπολογίζεται ως ~S_A - S_T~, όπου ~S_A~ οι πόντοι της Άννας από εδώ και πέρα και ~S_T~ οι πόντοι της Τάμτα αντίστοιχα. Προφανώς, η Άννα θέλει να μεγιστοποιήσει το σκορ ενώ η Τάμτα να το ελαχιστοποιήσει.

Γνωρίζοντας ότι και οι 2 θα παίξουν βέλτιστα, να βρείτε το τελικό σκορ.

Μορφή Εισόδου

Η πρώτη γραμμή περιέχει 2 ακεραίους ~N, M~.

Ακολουθούν ~N + 1~ γραμμές, η καθεμία με ~M~ δυαδικά ψηφία (χωρίς μεταξύ τους κενά): το ~j~-οστό ψηφίο της ~i~-οστής γραμμής είναι 1 αν και μόνο αν υπάρχει οριζόντια ακμή μεταξύ των τελειών στα σημεία ~(i, j),\ (i, j + 1)~

Ακολουθούν ~N~ γραμμές, η καθεμία με ~M + 1~ δυαδικά ψηφία στην παραπάνω μορφή: το ~j~-οστό ψηφίο της ~i~-οστής γραμμής είναι 1 αν και μόνο αν υπάρχει κατακόρυφη ακμή μεταξύ των τελειών στα σημεία ~(i, j),\ (i + 1, j)~.

Μορφή Εξόδου

Να εκτυπώσετε σε μοναδική γραμμή έναν ακέραιο, το τελικό σκορ.

Περιορισμοί - Υποπροβλήματα

• ~3 \leq N,M \leq 20~
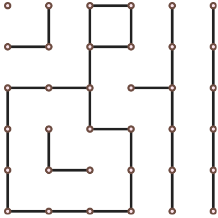
• Κάθε τετράγωνο έχει 0 ή 2 μη-σχεδιασμένες πλευρές

Έστω ότι συνιστώσα είναι μεγιστικό σύνολο μη-νικημένων τετραγώνων στο πλέγμα έτσι ώστε να μπορείς να μετακινηθείς μεταξύ τους μέσω των μη-σχεδιασμένων ακμών.

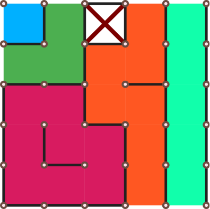
Βαθμολογία	Περιορισμοί
~20~	Υπάρχει μοναδική συνιστώσα
~20~	~N \cdot M \leq 12~
~20~	Υπάρχουν ακριβώς 2 συνιστώσες
~20~	~N, M \leq 7~
~20~	(χωρίς περαιτέρω περιορισμούς)

Παράδειγμα 1

Είσοδος:

3 3
000
111
011
110
1010
1000
1001

Έξοδος:

-5

Εξήγηση:

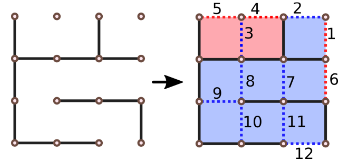
Παράδειγμα 2

Είσοδος:

5 5
00100
10100
11010
00100
01000
11100
011111
001011
101011
110111
100111

Έξοδος:

6

Εξήγηση: Αυτό το παράδειγμα αποτυπώνεται στην περιγραφή του προβλήματος.