Fountain

Ένα νέο συντριβάνι αποτελείται από ~N~ κατακόρυφα ευθυγραμμισμένα κυκλικά ρεζερβουάρ, αριθμημένα από πάνω προς τα κάτω ξεκινώντας από το 1. Ένα παράδειγμα φαίνεται παρακάτω:

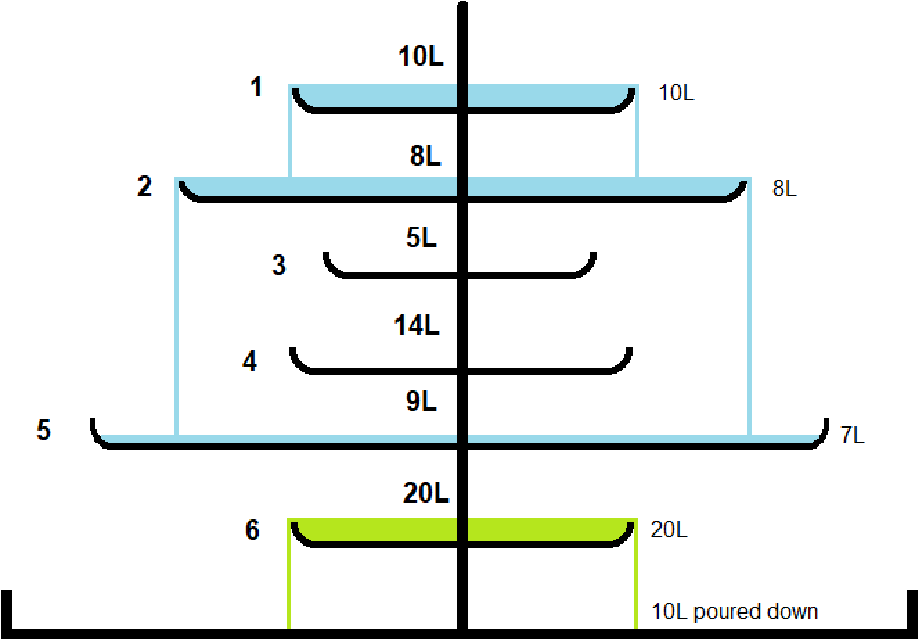
Κάθε ρεζερβουάρ έχει δοσμένη διάμετρο, χωρητικότητα και βρύση που μπορεί να απελευθερώσει οποιαδήποτε ποσότητα νερού σε αυτό. Όποτε η ποσότητα ξεπεράσει την χωρητικότητα του ρεζερβουάρ, το περισσευούμενο ξεχειλίζει από τα άκρα και πέφτει στο πλησιέστερο ρεζερβουάρ με γνησίως μεγαλύτερη διάμετρο. Αν δεν υπάρχει τέτοιο, καταλήγει στην καταβόθρα.

Σας ζητάται να απαντήσετε ~Q~ ανεξάρτητα ερωτήματα της παρακάτω μορφής: σε ποιο ρεζερβουάρ καταλήγει νερό χωρίς να υπερχειλίσει, αν η βρύση του ~R~-οστού ρεζερβουάρ εναποθέσει ~V~ λίτρα νερού. Αν το νερό καταλήξει στην καταβόθρα, να απαντήσετε ~0~.

Μορφή Εισόδου

Η πρώτη γραμμή περιέχει 2 ακεραίους ~N, Q~.

Οι επόμενες ~N~ γραμμές περιέχουν 2 ακεραίους ~D_i, C_i~: την διάμετρο και την χωρητικότητα του ~i~-οστού ρεζερβουάρ.

Οι επόμενες ~Q~ γραμμές περιέχουν 2 ακεραίους ~R_i, V_i~ που περιγράφουν το ~i~-οστό ερώτημα

Μορφή Εξόδου

Να εκτυπώσετε, σε ~Q~ διαφορετικές γραμμές, τις απαντήσεις των ερωτημάτων, στην σειρά που δίνονται.

Περιορισμοί - Υποπροβλήματα

• ~2 \leq N \leq 10^5~
• ~1 \leq Q \leq 2 \cdot 10^5~
• ~1 \leq C_i \leq 1,000~
• ~1 \leq D_i, V_i \leq 10^9~
• ~1 \leq R_i \leq N~

Βαθμολογία	Περιορισμοί
~30~	~N \leq 1,000,\quad Q \leq 2,000~
~30~	~D_1 < D_2 < \dots < D_N~
~40~	Κανένας επιπλέον περιορισμός

Παράδειγμα

Είσοδος:

6 5
4 10
6 8
3 5
4 14
10 9
4 20
1 25
6 30
5 8
3 13
2 8

Έξοδος:

5
0
5
4
2

Εξήγηση: Τα πρώτα 2 ερωτήματα φαίνονται στην εικόνα παραπάνω. Στο 3ο ερώτηματ δεν έχουμε υπερχείλιση στην καταβόθρα, καθώς τα ερωτήματα είναι ανεξάρτητα μεταξύ τους.