Iksevi

Μετά από δέκα χρόνια προγραμματισμού, ο Vinko αποφάσισε να αλλάξει επάγγελμα και να γίνει κεραμιστής. Ήδη από την πρώτη μέρα της νέας του δουλειάς ανέλαβε ένα εξαιρετικά δύσκολο έργο.

Πρέπει να στρώσει το δάπεδο της αίθουσας συναυλιών με τετράγωνα κεραμικά πλακίδια. Ωστόσο, δεν θα στρώσει το δάπεδο έτσι ώστε τα πλακάκια να είναι παράλληλα με τους τοίχους της αίθουσας. Αντίθετα, θα τα περιστρέψει έτσι ώστε οι διαγώνιοι των πλακιδίων να είναι παράλληλες με τους τοίχους.

Ο Vinko δεν έχει αποφασίσει ποιο μέγεθος πλακιδίων θα χρησιμοποιήσει, αλλά ξέρει ότι όλα πρέπει να έχουν το ίδιο μέγεθος και ότι το μήκος των διαγωνίων τους σε χιλιοστά πρέπει να είναι θετικός άρτιος αριθμός. Θα βάλει το πρώτο πλακίδιο έτσι ώστε να αγγίζει τον κάτω και τον αριστερό τοίχο και μετά θα στρώσει τα άλλα έτσι ώστε να μοιράζονται μια πλευρά με μερικά από τα πλακάκια που είχαν τοποθετηθεί προηγουμένως. Θα επαναλάβει τη διαδικασία μέχρι να στρώσει ολόκληρο το δάπεδο, του οποίου οι διαστάσεις είναι ~10^7 \times 10^7~ τετραγωνικά χιλιοστά.

Εκτός από καλός προγραμματιστής και κεραμίστας, ο Vinko είναι και εξαιρετικός μουσικός. Εξαιτίας αυτού, γνωρίζει ότι υπάρχουν ~n~ σημεία στο πάτωμα που είναι κρίσιμα για την καλή ακουστική στην αίθουσα. Η ακουστική της αίθουσας θα βελτιωνόταν σημαντικά εάν η γωνία ενός πλακιδίου βρίσκεται σε ένα από τα ~n~ σημεία.

Η αριστερή εικόνα δείχνει το πλακόστρωτο του οποίου τα πλακάκια έχουν διαγώνιο μήκους ~4~. Στο σημείο ~(2, 4)~ που είναι στη γωνία ενός πλακιδίου, η ακουστική είναι καλή, αλλά στα σημεία ~(4, 3)~ και ~(5, 1)~ δεν είναι.

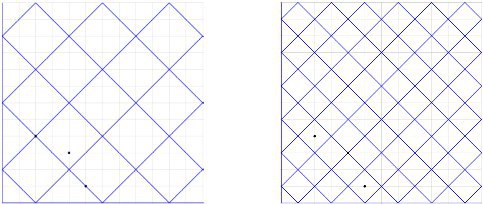
Η δεξιά εικόνα δείχνει το πλακόστρωτο του οποίου τα πλακάκια έχουν διαγώνιο μήκους ~2~. Το σημείο ~(4, 3)~ βρίσκεται στη γωνία ενός πλακιδίου, ενώ τα σημεία ~(2, 4)~ και ~(5, 1)~ όχι.

Βοηθήστε τον Vinko να καθορίσει για καθένα από τα ~n~ σημεία με πόσους τρόπους μπορεί να στρώσει το δάπεδο (δηλαδή, πόσες διαφορετικές διαστάσεις των πλακιδίων μπορεί να επιλέξει) έτσι ώστε το ~i~οστό σημείο να βρίσκεται σε μια γωνία πλακιδίων.

Είσοδος

Η πρώτη γραμμή περιέχει τον ακέραιο ~n~ ~(1 \le n \le 10^6)~, τον αριθμό των σημείων καλής ακουστικής.

Οι ακόλουθες ~n~ γραμμές περιέχουν δύο ακέραιους αριθμούς ~x_i, y_i~ ~(0 \le x_i, y_i \le 10^7)~, που υποδηλώνει ότι το ~i~-οστό σημείο απέχει ~x_i~ χιλιοστά από τον αριστερό τοίχο και ~y_i~ χιλιοστά από τον κάτω τοίχο της αίθουσας.

Έξοδος

Στην ~i~-οστή των ~n~ γραμμών εκτυπώστε τον αριθμό από τη δήλωση του προβλήματος για το ~i~-οστό σημείο.

Βαθμολογία

Υποπρόβλημα	Βαθμοί	Περιορισμοί
1	15	~1 \le n \le 10\,000,\,0 \le x_i, y_i \le 100~
2	55	~1 \le n \le 10\,000~
3	40	Κανένας επιπλέον περιορισμός.

Παραδείγματα

input

3
1 4
0 0
0 9

output

1
0
3

input

3
5 1
4 3
2 4

output

0
1
1

Επεξήγηση του 2ου παραδείγματος:

Οι εικόνες από τη δήλωση του προβλήματος αντιστοιχούν στο δεύτερο παράδειγμα.